実験内容
- 対象者 博士号を持つ40人
★資金管理が与える影響の知識はない - 勝つ確率 60%（コンピューターゲーム）
- 手持資金 1,000ドル
- 勝負回数 100回（毎回の賭け金は自由）
最終的に元の1,000ドルより増えたのは40人中（ ）人。
《詳細》
実験結果：２人（つまり勝者は５％のみだった）
《詳細を隠す》
ギャンブラーの誤謬とは？
《詳細》
ある事象の発生頻度が高かった場合、その後発生確率が低くなる
（あるいは逆に、ある事象の発生頻度が低かった場合に、その事象の発生確率が高くなる）と信じてしまうという誤謬。
観察される結果が真にランダムで、それぞれの試行が独立した確率過程である場合には、このような考えは誤りである。
（コイン投げ）
- １０回続けて表が出た場合、１１回目は裏が出やすいと思ってしまうが、やはり確率は５０％。
- ５人続けて男が産まれた場合、６人目は女が産まれやすいと思ってしまうが、基本的に確率はそれまで同様。
《詳細を隠す》
プロのギャンブラー
「勝ち」の何たるかを知っている
- 勝ち続きの時：たくさん賭ける
- 負けが込んでいる時：少なめに賭ける
普通の人
相場が4日連続上昇すると次は下げると予想する偏見など
- 負け続けの時：たくさん賭ける
- 勝った時：賭け金を減らす
例えば：
- ランダムに起きたに過ぎないトレンドがいつかは変わるものと信じる
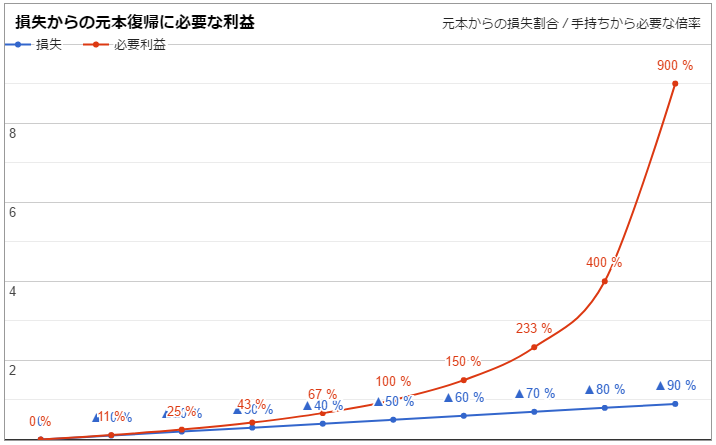
（上げが下げの根拠になっているとは限らない）- 3回続けて100ドル負けたら次は勝てるはず（勝率60%）と、300ドルの負けを取り戻すために400ドルを賭けるといったプロギャンブラーと逆の行動
パターン（例）
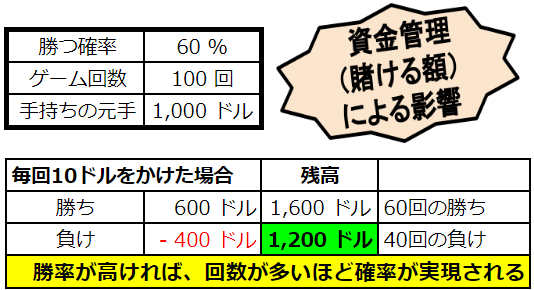
毎回10ドルずつ賭けることでサイズ調整を行う確率を味方につけるギャンブラーと、最大の結果を出したいがゆえに、資金量に対して1回に100ドルと大きめに賭ける欲望からの行動との比較。
上の様に1回10ドルで100回売買するような回数が多いと確率は実現されやすい…つまり結果が60%の勝率となる可能性が高くなる。
大き目のサイズで始めた場合
大きく掛けた方がリターンが大きい、又は多く取り戻せる
・・・と思ってしまう！
1回100ドル（最大10回しかできな）と大き目の賭け方をした場合、勝率60％の確率は実現されにくくバラツキが大きくなる…つまり60％の勝率は実現されにくく負けが続くことがある。
- 最初の3回で300ドルを失った場合
既に残高700ドル
→ここから60%の勝率とした場合、取り戻せる確率は低い。 - 更に4回で400ドルを失った場合
既に残高300ドル
→ここから60%の勝率とした場合、取り戻せる確率は困難。
最初に大きく負け上記の様に手持ちが300ドルになった場合、そこから同様に60%の勝率で100回のチャンスを与えられたとしても取り戻せる可能性は（確率的に）低い。
300ドル（手持ち）＋600ドル（勝ち）ー400ドル（負け）＝500ドル（残高）
一定範囲を超える損失の落とし穴？
こんにちは！ココモの唐沢です。
増益については、夢のある複利の話がよく登場しますが、損が出た場合はどうでしょう？この理屈はビジネス一般...
2017-05-02 19:17
